2.5 寻找环形链表和环入口的推导过程

问题

142. 环形链表 II

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

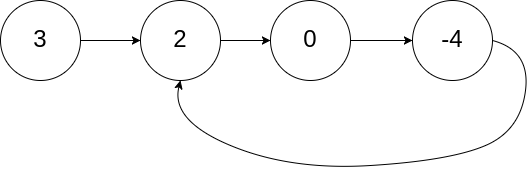
输入：

head = [3,2,0,-4], pos = 1  

输出：

返回索引为 1 的链表节点  

解释： 链表中有一个环，其尾部连接到第二个节点。

示例 2：

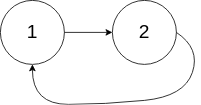
输入：

head = [1,2], pos = 0  

输出：

返回索引为 0 的链表节点  

解释： 链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：

head = [1], pos = -1  

输出：

返回 null  

解释： 链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引

**进阶：**你是否可以使用 O(1) 空间解决此题？

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* detectCycle(ListNode* head) {
    
    }
};

分析

哈希存址法

想要知道链表是否有环，则需要确定判断条件，判断是否有环的条件，从环的拓扑上来说，就是一个数量在1以上的链表的next总是指向下一个节点，然后这下一个节点是之前的其中一个节点，从遍历的特征上来看，单链表会陷入循环中。

也就是说，如果每次遍历的时候，都保存之前的节点地址，只要在节点大于1的时候，下一个节点地址是之前保存的节点地址，那么，节点就存在环，首次发现节点地址重复出现的地方即为环的入口，为了缩减查找耗时，可以使用HASH表保存之前的地址。
但是，这样子的话，随着节点数量K的增加，占用的内存会变成O(K)，题目要求需要使用 O(1) 的空间复杂度来解决问题，因此有没有办法让之前节点地址不进行保存，或者只保存最少的固定的部分以实现O(1)的空间复杂度呢？

快慢指针法

如果之前的节点地址不进行保存的话，那么是无法判断链表是否有环的（因为单链表地址无法和任何东西进行比较），无法比较就无法判断，无法判断就没办法消除是否有环的不确定性。

因此为了进行比较，至少要保存之前的（部分）地址。

为了解决此问题，使用两个速度不一样的指针。

快慢指针法就像是两个不同速度的运动员在环行跑道跑步，把问题转化成为了追及问题。

起点相同查找环

当节点A每次前进1步，如果有环，设定环入口为$Q_E$，环的长度为$S_Q$，那么节点A总是能回到环入口$Q_E$。
无论加入多少不同速度的节点进行步进，从环入口出发，新增的节点总是能回到环入口$Q_E$。
在节点A总是不停步进的情况下，如果再引入一个速度“更快”但是速度不变的节点B，这个更快的节点相对于原节点的速度设定为k。

那么如果他们同一点出发，当节点A走完1圈的时候，节点B也会走完k圈，这样的话，他们就会在入口相遇。
这时候可以通过二者的地址判断是否相同，相同的话，就认为链表有环。

起点不同查找环

现在考虑如果是从不同点同时出发，假设二者之间的距离为$D_{AB}$，B总是比A多走1步，如果A走完1圈的时候，节点B也会走完2圈，但是并不会相遇，想要相遇，就必须让节点B，多走$D_{AB}$的距离。

假设节点B移动后的位置是$D_B$，节点A移动后的位置是$D_A$，让A点作为环的起点，B点领先A点$D_{AB}$距离，设定m为整数，$S_Q$为环的长度。

现在如果能搞清楚$D_A$和$D_B$的关系，就能知道相遇条件。
设A的速度为$V_A$ ，每次只走1步，那么$V_A=1$，设定A走过的步数为t，那么A新位置为： $D_A=V_A\ast t=t$
设B的速度为$V_B$，那么B走过的距离为：$D_B=V_B\ast t$
根据已知条件，B总是比A快u倍，因此：$V_B=u\ast V_A$
考虑到B位置是在$D_{AB}$处，因此有B的新位置为：

$$\begin{array}{rl}{D}_B& =V_B\ast t+D_{AB}\\ & =u\ast V_A\ast t+D_{AB}\end{array}$$

B比A快1步的时候，u=2，即B新位置为：

$$\begin{array}{rl}{D}_B& =2\ast 1\ast t+D_{AB}\\ & =2t+D_{AB}\end{array}$$

因为移动的步数等于环长$S_Q$的时候，会回到原来位置，将A相对于起点的位置设为$X_A$，B相对于起点位置设置为$X_B$，易知在起始位置的时候$X_A=0$，$X_B=D_{AB}$，那么有：

$$\begin{array}{rl}{D}_A& =X_A+m_1\ast S_Q=t\\ D_B& =X_B+m_2\ast S_Q=2t+D_{AB}\end{array}$$

即：

$$\begin{array}{rl}{X}_A& =D_A+m_1\ast S_Q\\ & =t+m_1\ast S_Q\\ & \\ X_B& =D_B+m_2\ast S_Q\\ & =2t+D_{AB}+m_2\ast S_Q\end{array}$$

其中$m_1$和$m_2$是整数，$m_1$​ 和 $m_2$​ 分别表示走过整圈的次数，它们的选取使得 $X_A$ 和 $X_B$​ 均落在区间 $[0,S_Q)$ 内。

当B比A多走$B_{AB}$距离的时候，他们就会相遇，可以知道相遇条件为：

$$\begin{array}{rl}{X}_A& =X_B\end{array}$$

综合上式可得：

$$t+m_1\ast S_Q=2t+m_2\ast S_Q+D_{AB}$$

即：

$$\begin{array}{rl}t+D_{AB}& =(m_1-m_2)\ast S_Q\\ & =n\ast S_Q\end{array}$$

其中$n=(m_1-m_2)$是整数。 这个公式的含义是，当走过的步数和AB距离的和等于环的长度的倍数时候，也就是B多走的步数为$t=n\ast S_Q-D_{AB}$ 时候，AB就会相遇。

现在用数学归纳法进行证明。

基步证明：证明 $n=1$ 的时候，条件成立。

取$n=1$，这时$t=S_Q-D_{AB}$
这时有：

$$\begin{array}{rl}{D}_A& =X_A+m_1\ast S_Q\\ & =t\\ & =S_Q-D_{AB}\\ & \\ D_B& =X_B+m_2\ast S_Q\\ & =2t+D_{AB}\\ & =2(S_Q-D_{AB})+D_{AB}\\ & =S_Q-D_{AB}+S_Q\end{array}$$

即：

$$\{\begin{array}{ll}{X}_A& =S_Q-D_{AB}\\ m_1& =0\\ X_B& =S_Q-D_{AB}\\ m_2& =1\end{array}$$

故有：

$$X_A=S_Q-D_{AB}=X_B$$

即经过$t=S_Q-D_{AB}$步的时候，A和B相遇在 $S_Q-D_{AB}$处相遇，即基部成立。

代个容易理解的数值的话，表示如下：
可取$S_Q=5$, $D_{AB}=2$ 的时候，那么在t=3步的时候，AB就能相遇。
这时候有：

$$\{\begin{array}{l}{D}_A=3\\ X_A=3\\ D_B=6+2=3+5\\ X_B=3\end{array}$$

也就是这时候相遇的位置是 3 。

假设 $n=k$ 的时候，$X_A=X_B$ 也成立，其中k正整数。

当$n=k$ 的时候，有：

$$\begin{array}{rl}t& =k\ast S_Q-D_{AB}\\ & =S_Q-D_{AB}+(k-1)\ast S_Q\end{array}$$

这时有：

$$\begin{array}{rl}{D}_A& =X_A+m_1\ast S_Q\\ & =t\\ & =S_Q-D_{AB}+(k-1)\ast S_Q\\ & \\ D_B& =X_B+m_2\ast S_Q\\ & =2t+D_{AB}\\ & =2(S_Q-D_{AB}+(k-1)\ast S_Q)+D_{AB}\\ & =S_Q-D_{AB}+(2k-1)\ast S_Q\end{array}$$

即：

$$\{\begin{array}{ll}{X}_A& =S_Q-D_{AB}\\ m_1& =k-1\\ X_B& =S_Q-D_{AB}\\ m_2& =2k-1\\ X_A& =X_B\end{array}$$

当 n = k 成立的时候，证明 n = k + 1 也成立

当n = k+1的时候，有：

$$\begin{array}{rl}t& =(k+1)\ast S_Q-D_{AB}\\ & =S_Q-D_{AB}+k\ast S_Q\end{array}$$

这时有：

$$\begin{array}{rl}{D}_A& =X_A+m_1\ast S_Q\\ & =t\\ & =S_Q-D_{AB}+k\ast S_Q\\ & \\ D_B& =X_B+m_2\ast S_Q\\ & =2t+D_{AB}\\ & =2((k+1)\ast S_Q-D_{AB})+D_{AB}\\ & =S_Q-D_{AB}+(2k+1)\ast S_Q\end{array}$$

则：

$$\{\begin{array}{ll}{X}_A& =S_Q-D_{AB}\\ m_1& =k\\ X_B& =S_Q-D_{AB}\\ m_2& =2k+1\\ X_A& =X_B\end{array}$$

即当 n = k+1 的时候，经过 $t=S_Q-D_{AB}+k\ast S_Q$步，这时A和B相遇，相遇点在$X_A=X_B=S_Q-D_{AB}$。

也就是说，一个速度为1的指针A和另一个速度为2的指针B，在相距$D_{AB}$的距离同时出发，如果链表有环，那么二者必然相遇，相遇的位置在$S_Q-D_{AB}$处，其中$S_Q$为环长。

快指针速度的推广

当B比A快u倍，而u不为2的时候，容易推广出u为任意倍数的情况：

那么有公式：

$$\begin{array}{rl}{D}_A& =X_A+m_1\ast S_Q=t\\ D_B& =X_B+m_2\ast S_Q=ut+D_{AB}\end{array}$$

得到：

$$\begin{array}{rl}{X}_A& =D_A+m_1\ast S_Q\\ & =t+m_1\ast S_Q\\ & \\ X_B& =D_B+m_2\ast S_Q\\ & =ut+D_{AB}+m_2\ast S_Q\end{array}$$

当A和B相遇时有：

$$\begin{array}{rl}{X}_A& =X_B\end{array}$$

这时候可得：

$$t+m_1\ast S_Q=ut+m_2\ast S_Q+D_{AB}$$

即：

$$\begin{array}{rl}(u-1)t+D_{AB}& =(m_1-m_2)\ast S_Q\\ & =n\ast S_Q\end{array}$$ $$t=\frac{S_Q-D_{AB}}{u-1}+\frac{(n-1)}{u-1}\ast S_Q$$

其中$n=(m_1-m_2)$是整数。 这个公式的含义是，经过 $\frac{S_Q-D_{AB}}{u-1}+\frac{(n-1)}{u-1}\ast S_Q$步时，A和B相遇，相遇点在$X_A=X_B=\frac{S_Q-D_{AB}}{u-1}$。 需要注意的是，当 $u=1$ 的时候，没有意义，公式和步数无关，也就是说，环内两个不同出发点，但是速度相同的指针永远不会相遇。

寻找环入口

当u=2， A和B同时前进，当A到达环入口的时候，B刚好走过2倍A的距离，设起点为C点，设环入口为0点，那么A到达入口的时候，有入口位置 $0$，A经过的距离设定为$C_A$，B经过的距离设定为$C_B$，因为B是A的2倍速度，
因此有：

$$C_B=2C_A$$

因为A只走过$C_A$距离，换而言之，B在进入环内后，又多走了$C_A$的距离，也就是说，B在环内的$C_A$位置。
当A刚好进入环入口的时候，设定B相对于A的位置为$D_{AB}$，令环长$S_Q$ ，容易知道：

$$C_A=D_{AB}+m_5\ast S_Q$$

其中$m_5$是整数，用于保障B的终点$D_{AB}$在区间 $[0,S_Q)$ 内。
在这时候，A在环的入口，让A和B同时继续移动，因为参考系相同的缘故，这时候可以套用起点不同查找环中的方法，可以知道，当A和B相遇的时候，A和B是在节点内的$X_A=X_B=S_Q-D_{AB}$位置。

在这时，在起点C位置新增一个每次步进1位的节点C，节点C和节点A速度一样，节点C和节点A同时出发，当节点C到达环入口的时候，移动了$C_A$距离。这时候节点C的位置是在0点，即$X_C=0$。
这时，节点A同样也移动了$C_A$的距离，节点A累计移动的距离：

$$\begin{array}{rl}{D}_A& =X_A+m_1\ast Q_S\\ & =C_A+S_Q-D_{AB}\\ & =D_{AB}+m_5\ast Q_S+S_Q-D_{AB}\\ & =(m_5+1)\ast Q_S\end{array}$$

其中 $m_1$用于保证节点A的位置$X_A$在区间 $[0,S_Q)$ 内。
即：

$$\{\begin{array}{l}{X}_A=0\\ m_1=m_5+1\end{array}$$

这时节点A刚好也到达了环的入口。也就是$X_A=X_C=0$

也就是说，一个速度为1的指针A和另一个速度为2的指针B在同一个初始位置同时出发，当A和B相遇的时候，在初始位置再增加1个速度为1的指针C，再让指针A和C同时前进，指针A和C就会在环的入口相遇。

代码

这里只给出快慢指针法的代码。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* detectCycle(ListNode* head) {
	    ListNode* first = head;
	    ListNode* second = head;
	    bool hasCycle = false;
        while (second && second->next) {
            first = first->next;
            second = second->next->next;
            if (first == second) {
                hasCycle = true;
                break;
            }
        }
        if (hasCycle) {
            ListNode* three = head;
            while (first != three) {
                three = three->next;
                first = first->next;
            }
            return three;
        }
        return nullptr;
	}
};

*****